Miguel Lurgi
16 December 2025
This week I once again had the pleasure to share the lab’s research with scientists from around the world at the Annual Meeting of the BES, this year in Edinburgh!

With countless interesting talks and posters, thematic sessions and just the vibrant atmosphere, this meeting is always a chance to catch up with friends and colleagues on the latest developments of our research and have fun while doing it. This year, I also contributed in other ways by joining a focus group where we discussed the impact of the Annual Meeting on our research and on ecological science. Thanks Rachel for the chance to join this group!
I also chaired a session on Evolutionary Ecology: Plasticity, dispersal and ecological responses which was full of interesting talks and discussions from the impact of adaptive dispersal on population persistence to the evolution of sex ratios in breeding systems.
During my poster presentation on the Coevolutionary drivers of phylosymbiosis and microbiome divergence in host-microbe associations, I had the chance to discuss with several interesting people our ideas on the origins of complex symbioses and how we can develop quantitative mathematical models to better understand them.
Before heading back to Swansea I had some time to check out the Christmas market and other nice sightings in the city centre of Edinburgh. A very nice town! And of course, to head down to the pub, or catch up at the venue, with old friends from all over the world.
Thanks to the Leverhulme Trust (through project grant RPG-2022-114) for the support to attend and present my work at this meeting.
Miguel Lurgi
29 November 2025
For a few days this November I was very lucky to be part of a research expedition to the Kartong Bird Observatory in The Gambia. I had the opportunity to learn more about the projects they are running from the population genetics of a couple of species of vultures (Hooded Necrosyrtes monachus and White-backed Gyps africanus) to the migration patterns and wintering ecology of nightingales Luscinia megarhynchos. Many inspirational ideas emerged from this for potential future research projects at Kartong touching the applied side of the research we develop at the Computational Ecology Lab.



The expedition was a success, with around 3450 individual birds from 154 different species recorded. These data constitute a valuable contribution to bird research in The Gambia and more generally for a better understanding of bird populations worldwide.
As an added bonus I enjoyed very much the ringing and the birdwatching, with so many species observed in amazing habitats. I had the opportunity to join ringing teams both on terrestrial as well as wetland and estuarine environments. Everyday presented new chances to see and experience different locations and different species, from the massive flocks of Western Reef Egretta gularis, Black Egretta ardesiaca, Striated Butorides striata, Squacco Ardeola ralloides and Black-headed Ardea melanocephala herons that roamed the grasslands of Batabar, to the Grey Pluvialis squatarola, Common Ringed Charadrius hiaticula and White-fronted Charadrius marginatus plovers as well as Whimbrels Numenius phaeopus and Common Actitis hypoleuca, Green Tringa ochropus and Wood Tringa glareola sandpipers of the coastal and mangrove habitats of Barracunto and Stala. Not to mention the beautifully coloured birds found across the entire reserve such as Little Merops pusillus, Blue-cheeked Merops persicus and Swallow-tailed Merops hirundineus bee-eaters, Yellow-crowned Gonoleks Laniarius barbarus, Senegal Coucal Centropus senegalensis, Beautiful Sunbird Cinnyris pulchellus, Red-cheeked Cordonbleu Uraeginthus bengalus amongst many others!




On the personal side, beyond the ringing, it was great to get to meet and interact with an incredible team of researchers and expert ornithologists such as Michael, Emmanuel, Naffie, Olly, Roger, and many others. I am really grateful for their guidance and the knowledge imparted during the expedition. It was great to be part of the team.




I had an amazing time as part of the Swamp Squad, paddling around puddles and getting into deep ponds for which my thigh waders were not enough! Always in the search for nice species such as White-faced whistling ducks Dendrocygna viduata, Greater Painted-snipe Rostratula benghalensis, and of course Ospreys Pandion haliaetus!
Thanks to all the team for an unforgettable experience and especially to the Swamp Squad, my bro Billy who was always making the time enjoyable, and the people of Kartong! Hope to be back soon.
Photo credits: Purple Heron, Goliath Heron and Crocodile kindly provided by Laura Raven and John. White-fronted Plover, Long-tailed Nightjar, Senegal Coucal, Singing Cisticola and African Fish Eagle kindly provided by Noelia D. Alvarez and Ricki McCloud. Thanks for letting me use your pictures guys!
Miguel Lurgi
03 November 2025
Today I had the pleasure to share my research on the modelling of complex ecosystems across scales with the researchers and students at the School of Biosciences of the University of Sheffield.

In my talk on Cross-scale community assembly: from microbiomes to spatial food webs, I presented some of our recent findings on the eco-evolutionary theoretical framework we are developing to unveil the origins of complex symbioses. I then moved on to larger ecological scales and discussed some results on the spatial modelling of complex food webs and the effects of perturbations on their stability and organisation.
Before heading back to Swansea I had some time to check out the pair of peregrine falcon around St George’s church!
I would like to thank Oscar for the kind invitation and for organising the visit. Also, to Andrew and his group for the great discussions and the great dinner out after the seminar. Hope to visit again soon!
Miguel Lurgi
25 October 2025
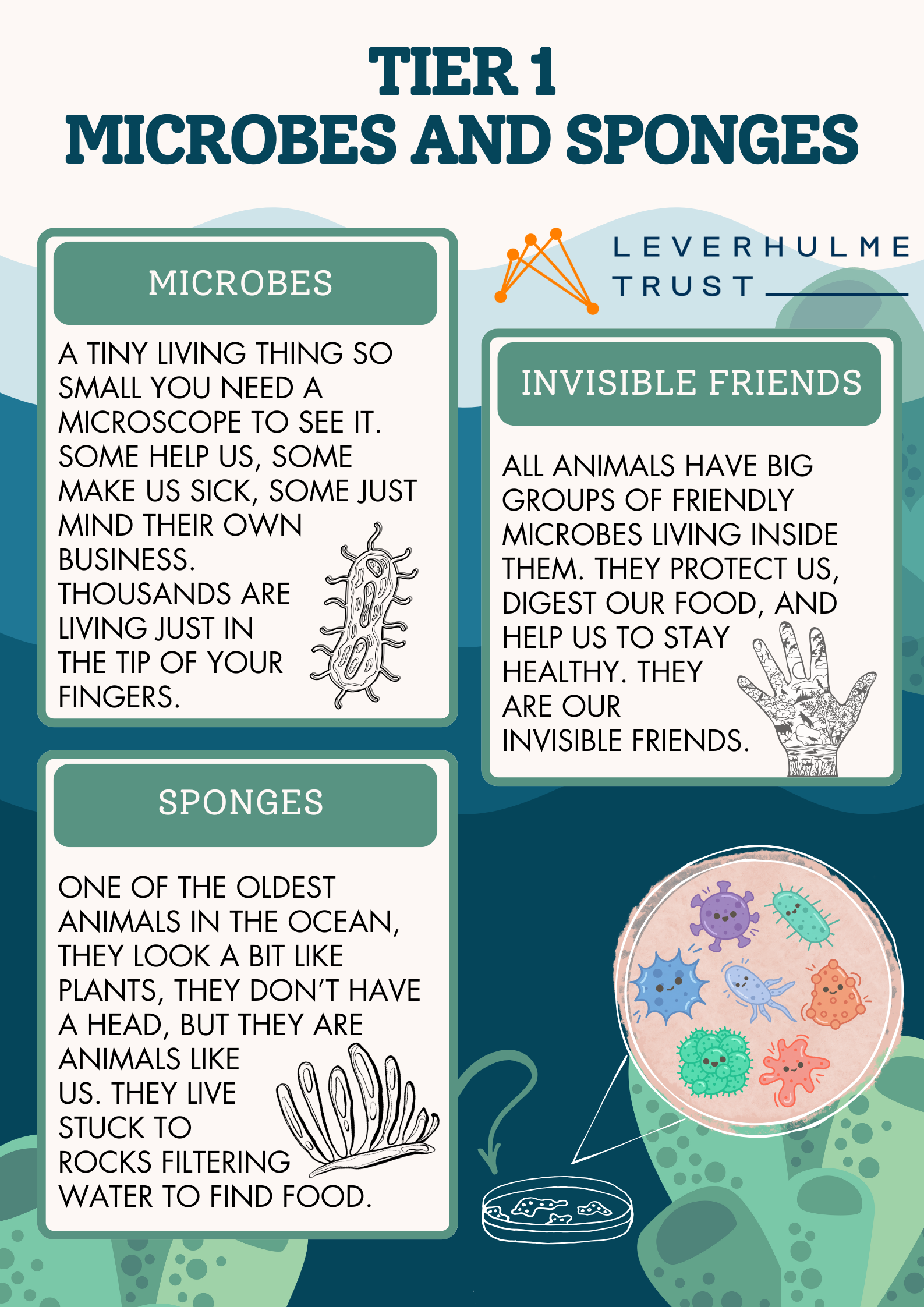
This weekend we were delighted to present our research at the annual Swansea Science Festival. It was a great opportunity to talk about microbes, sponges and microbial communities to kids, parents and attendees of all ages. We even had some visitors from the Star Wars world who wanted to know more about microbiomes!
Our stand was full of engaging activities from soft toys that looked like microbes and kids could sort into handcrafted sponges to build-your-own microbiome crafts for children!


We also had microscopes with an assortment of slides that everybody could use to have a look at the microscopic structures of plant, animals, and even bacteria, our invisible friends that do so much for our survival and the wellbeing of our planet.
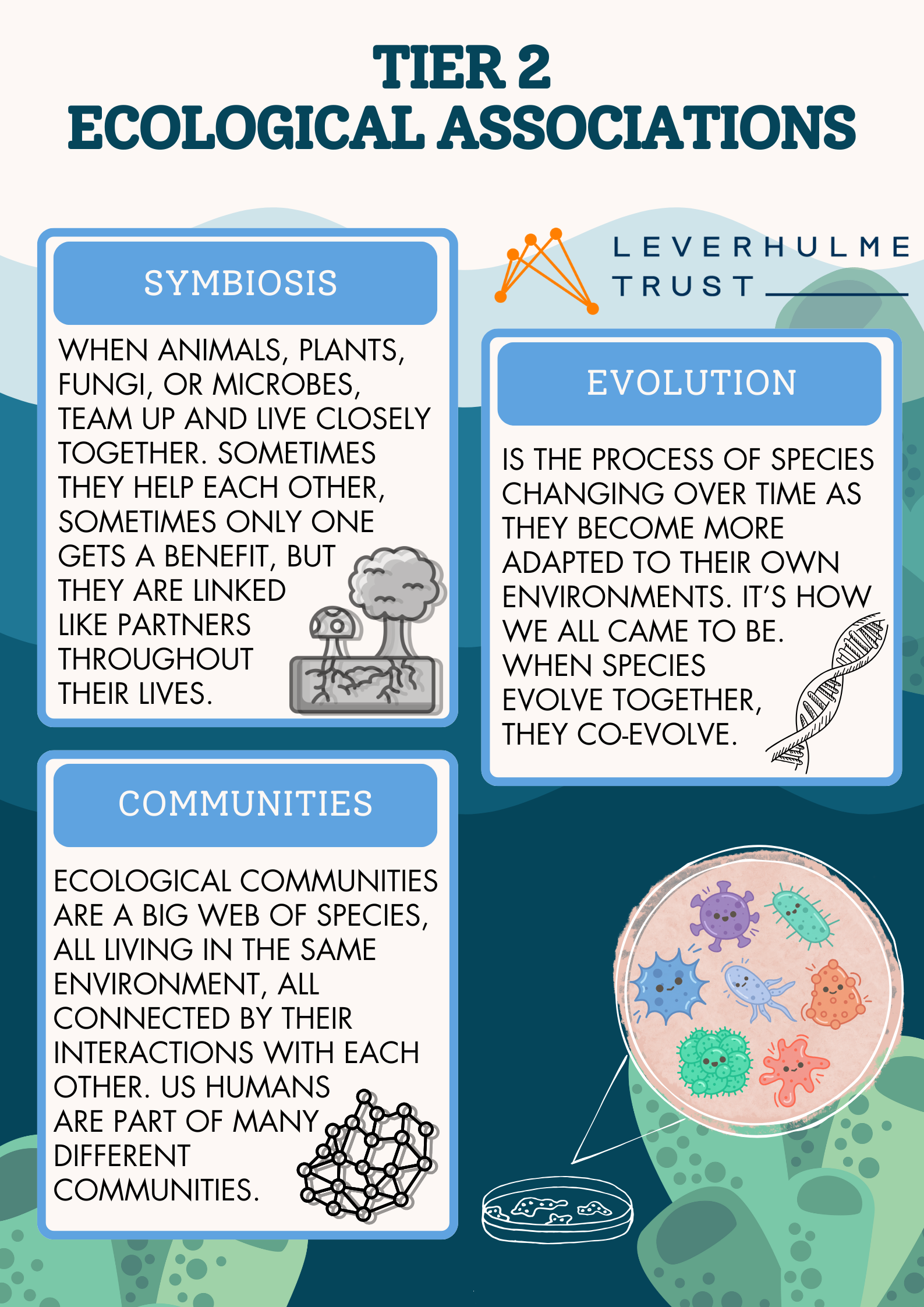
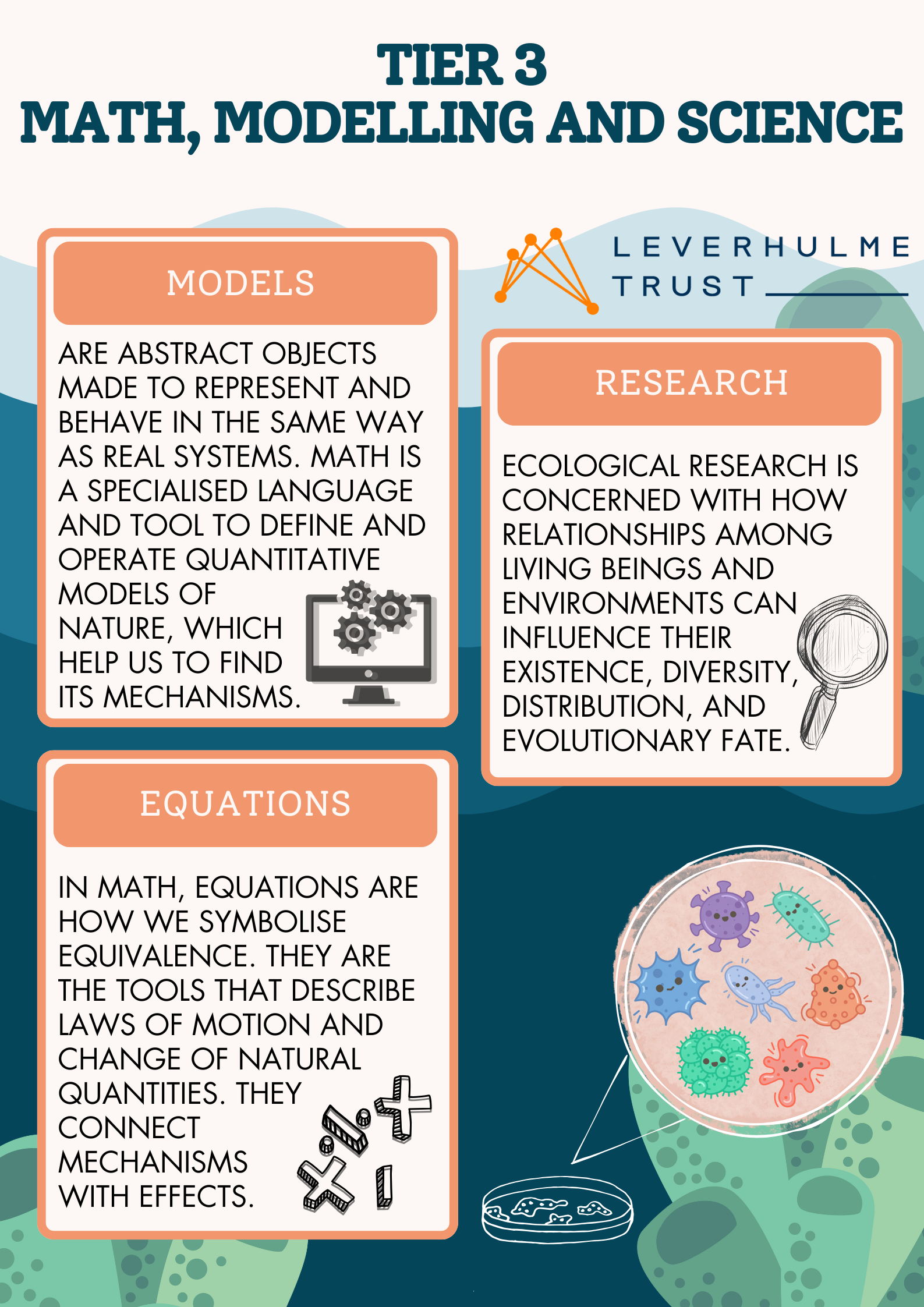
For those more interested in the science behind it all we also had informative flyers to take home detailing how we go from thinking about microbes and marine sponges to abstracting those associations into concepts of evolution, metacommunities and symbioses. We then built up all the way to a 3rd tier of complexity linking those concepts to mathematical equations and models that help us reason about these complex, yet fundamental ecosystems that persist all around us and without which life on Earth would not be possible.
At the end of the day we got a wall full of handcrafted microbiomes from all the kids that visited our exhibit. All in all it was great fun!

The Leverhulme Trust supported our stand at the Science Festival through Research Project Grant RPG-2022-114 to ML.
Thanks to Gui, Jooyoung and Olivia for all your help. And thanks to the organisers, and Delyth in particular, for a great festival.
Miguel Lurgi
01 October 2025
We started this term with a nice invitation to present our work on the modelling of the evolution of microbiomes at the Colloquium of the Centre for BioMathematics at Swansea University. In this talk, Gui presented our current work on a stochastic framework for community assembly in which complex microbial communities are assembled during ecological timescales and future generations of inherited microbiomes are seeded from these across evolutionary timescales.

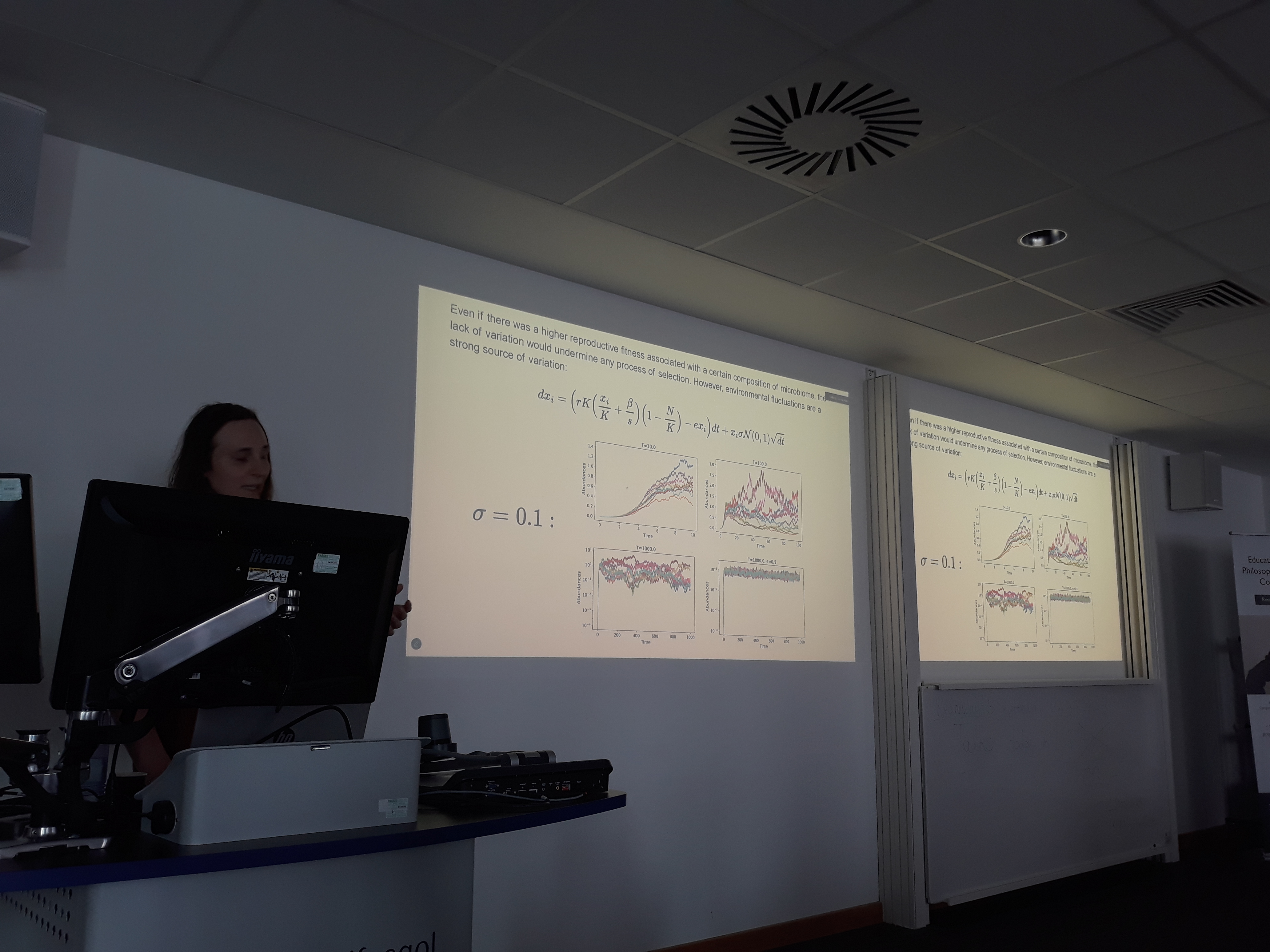
These coupling of timescales produces a variety of rich dynamics that allow us to explore the processes by which complex microbiomes associated to multicellular organisms are assembled. The model introduces fitness dependencies of hosts on the performance of microbial communities, as well as the evolution of carrying capacity and vertical transmission. These ingredients are sufficient to produce the complex associations we observe in natural systems such as marine sponges.
The presentation provided interesting grounds for follow up discussions both during the session and afterwards in one-to-one sessions with members of the Mathematics Department, generating new synergies and potential collaborations across research groups!
Special thanks go to Noemi and Valeria for hosting us at the Computational Foundry and providing tea and biscuits! :)




















